Exams are considered to include an element of suspense before the exam and an element of surprise after the question paper is received. However, the element of surprise can be mitigated if the element of preparedness is strong. This guide focuses on offering a complete overview of all the key topics of SAT Maths formulas. We’ll go over the section’s structure, focus on understanding the basics of SAT math, and talk about some crucial success tactics.

An Overview of the SAT Maths Test

The SAT math question is taken from four different sections of mathematics and contributes different percentages

• Algebra- 35% (13-14 questions) 
• Advance math- 35% (13-14 questions) 
• Problem-solving and Data analysis- 15% (5-7 questions) 
• Geometry and trigonometry- 15% (5-7 questions) 

Importance of SAT Maths Formulas in Acing the Math Section

Mastery of the fundamental SAT math concepts provides a crucial foundation for effectively addressing even the trickiest application problems. Here are some key points on the importance of formulas for answering SAT Math questions

• Saves time – By understanding the fundamental concepts and formulas, you avoid wasting valuable minutes trying to derive them from scratch during the test. This speeds up your problem-solving capacity. 

• Avoids mistakes – Under pressure, attempting to remember or derive formulas could result in inaccuracies that are minor but expensive.

• Allows deeper focus – Since you can recall your formulas easily, it will give you the benefit of concentrating effectively on problem-solving logic.

• Facilitates strategy Armed with a set of foundational formulas, you can quickly determine which ones to apply to a particular question and strategically use them.

• Covers a vast range of topics– The SATs have a very broad range of math topics, so knowing formulas across algebra, geometry, trigonometry, statistics and more is the key.

• Enhances confidence Having a firm grasp of formulas makes you feel prepared and at ease during the test, as opposed to nervous. Gains in points may result from this confidence.

General Tips For Memorizing And Applying SAT Maths Formulas

Mastering the entire list of digital SAT math formulas can be a daunting task. However, with the right tips and strategies, the entire process of memorizing the formulas can be managed easily. Here is a list of a few tips that will help 

• Prioritize Understanding Over Memorization While memorizing formulas can be beneficial, a thorough knowledge of their underlying principles is significantly more helpful for long-term retention and application. Instead of simply memorizing each formula, focus on understanding the logic behind it. 

• Use standardized review strategies Knowledge consolidation and memory preservation require frequent review. To help with recall and long-term memory connection, practice rewriting formulas or using spaced repetition apps or flashcards. 

• Encourage interconnection between formulas Understanding the connections between various formulas can greatly increase retention. Examine the relationships between formulas to create a coherent conceptual framework for your knowledge of the topic. This will improve your memory for and application of pertinent formulas in a variety of settings involving problem-solving. 

• Make practical application your top priority simply learning formulas by heart is not enough. Applying them actively to practice or real-world situations related to your goals—like the SAT—will help you master them. This procedure strengthens comprehension, encourages adaptability in problem-solving, and increases self-assurance in your capacity to apply the formulas successfully.

Conquer The Basics With Arithmetic And Number Properties 

This part explores the key ideas you’ll come across in SAT math Basic Arithmetic and Number Properties. You can refresh your memory on fundamental concepts such as exponent rules, rational and irrational numbers, integer characteristics, and order of operations in this section. These SAT math formulas are critical for success in problem-solving and efficiency during the exam.

 

Order of Operations (PEMDAS) 

PEMDAS stands for

• Parentheses First, check what’s inside the brackets.
• Exponents Secondly, solve powers and roots before.
• Multiplication and Division (from left to right) Now, solve these operations in the order they appear.
• Addition and Subtraction (from left to right) Lastly, perform these operations.

Properties of Integers (Even, Odd, Prime Numbers) 

Whole numbers make up integers. They could be zero, negative, or positive. Understanding these properties will aid you in solving issues requiring divisibility, factorization, and other concepts 

• Even numbers Divisible by 2 without a remainder (Ex- 2, 4, 6…).
• Odd numbers Not divisible by 2 (Ex- 1, 3, 5…).
• Prime numbers Only divisible by 1 and itself (Ex- 2, 3, 5, 7, 11…).

Rational and Irrational Numbers 

Understanding the characteristics of rational and irrational numbers will help you deal with problems requiring computations, proofs, and comparisons.

• Rational numbers Represented as fractions (a/b, where b ≠ 0), like 1/2 or 3/4.
• Irrational numbers Cannot be expressed as a fraction, like the square root of 2 or pi (π).

Exponent Rules and Roots

Powers and their inverses are the subject of exponents and roots. Understanding how exponents and expressions work and master root properties with the examples below- 

Algebra And Functions

This section gives you an overview of SAT math formulas by examining the ideas of algebra and functions, which are the basis of many questions asked in exams. 

Linear Equations and Inequalities

First-order equations are linear equations. In the coordinate system, the linear equations are defined for lines. A linear equation in one variable contains a homogeneous variable of degree 1, or just one variable. There might be more than one variable in a linear equation. It is referred to as a linear equation in two variables if there are two variables in it, and so on. 

Inequalities 

If two real numbers or algebraic expressions are related by the symbols “>”, “<”, “≥”, “≤”, then the relation is called an inequality.

Examples 

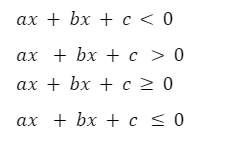
 System of equations

A system of linear equations is defined as two or more linear equations with two or more variables that are taken into consideration simultaneously.

For example, a set or collection of equations that are handled collectively is called a system of equations.

Both algebraic and visual solutions to these equations are possible.

The point where two lines intersect is the solution to the system of equations.

 Functions and their representations

Functions can be represented as 

f(x)= x²+2

Where, f is the function, (x) is the input  x²+2 and will give the output. 

It is always possible to graph functions, and the graphs produced by various function types will seem different. The x value is the graph’s input, while the y value is its output on a standard coordinate graph with x and y as its axes.

One output can have several inputs, but each input (y value) can only yield one output. Put otherwise, an output can be produced by a combination of inputs.

This implies that a function graph can have a single y-intercept but a possibility of several x-intercepts.

 Factoring and solving quadratic equations

Here, you are trying to find out what two binomials, when multiplied together, equal the expression.

Let us understand with this example;

x²+6x+9=0 

x²+3x+3x+9=0              (6x can be written as 3x+3x) 

x(x+3)+3 (x+3) =0

(x+3)(x+3)=0

(x+3)=0 or (x+3)=0 

x= -3 or x=-3 

Geometry and Measurement 

You’ll be tested on several geometry concepts on the SAT. To approach geometry problems as quickly and effectively as possible, you should first ensure that you have a firm grasp of the formulas and guidelines about all shapes, including area and perimeter. The ability to deduce the answer from hints in the question stems and figures are also crucial. We will attempt to cover every significant geometry topic related to the SAT math examinations in this part.

 Angles, Parallel Lines, and Polygons

Angles and Parallel Lines 

Two straight lines when stretched to infinity and never intersect, are known as Parallel lines, and represented as //. 

When a third line, like in the picture below, crosses two lines (which need not be parallel), the crossing line is known as a transversal

Now, if we draw two parallel lines and then a line transversal through them, we will have eight different angles shown below 

Together, the eight angles will create four sets of corresponding angles. One of the pairings in the above figure is made up of angles F and B. If both lines are parallel, then the corresponding angles are congruent. Corresponding pairs are all angles that are in the same position concerning the transversal and the parallel lines.

Interior angles are those that are between the two parallel lines, such as angles H and C above, but external angles are those that lie outside of them, such as angles D and G. 

Alternate angles are those that are on the opposing sides of the transversal,  like H and B. 

Adjacent angles are those that have a common ray and a shared vertex, such as angles G and F or C and B. In this situation, where the adjacent angles are generated by two intersecting lines, we get two sets of adjacent angles (G + F and H + E), which are both supplementary.

Vertical angles are two angles that are opposed to one another, such as D and B in the preceding image. Vertical angles are always congruent.

Polygons

Any enclosed, flat object composed entirely of straight lines is called a polygon. For a polygon to be considered “enclosed,” all of its sides must join, and it cannot have any curved sides, as shown in the figure below 

Polygons are of two types

• Regular polygon
• Irregular polygon

Regular polygons have equal sides and angles, whereas irregular polygons do not.

Examples of Regular polygons

Examples of irregular polygons

The number of sides and angles of any polygon form determines its name. A pentagon has five sides (called “penta” meaning five), a quadrilateral has four sides (called “quad” meaning four), and so on. A triangle has three sides and three angles (called “tri” meaning three).

Circle formulas (circumference, area)

Any shape’s circumference indicates the path or limit that encircles it. In other terms, the circumference is also known as the perimeter, which serves to determine the length of the outline of any shape. 

The circumference of a circle is equal to 2πR, where R is the circle’s radius and π is a mathematical constant with a value of 3.14.

An area is the space that a circle covers or the area that the circle itself surrounds.

To calculate the area of a circle, use the formula A = πr², where r represents the radius. This formula applies to all circles with varying radii.

Triangles

Less than 10% of all SAT math questions are triangle questions. Nevertheless, you still want to answer those questions correctly, so you should be ready to identify all types of triangles. 

Let’s start by discussing the fundamentals. Three straight lines joined at three angles to form a flat figure is called a triangle. These angles add up to 180°.

1. A triangle with equal sides and angles is called an isosceles triangle.

2. A triangle with three equal legs and three equal angles is called an equilateral triangle. 

3. When one of the triangle’s angles is 90°, the triangle is said to be right. Since the angles of a triangle always add up to 180°, this implies that the sum of the other two angles must also be 90°.

Volume and surface area of 3D shapes

The majority of solid geometry questions on the SAT are found toward the conclusion of each section. This means that solid geometry questions are regarded as some of the more difficult questions (or those that will take the longest to finish, as they frequently require numerous steps).

Even though many of the formulas are provided as shown in the figure above, you must comprehend how and why they operate. Therefore, pay attention to them to improve your understanding, and deepen your knowledge, but don’t worry too much about memorizing them.

Data Analysis, Statistics, and Probability

In this section, you will be tested on your analytical skills. Below we have shared a gist of some of the important topics to be considered in this section. 

 Interpreting and analyzing data (mean, median, mode)

A mean is a statistical average that can be calculated by adding up all of the numbers in a group and dividing the result by the total number of numbers in the group.

The number that falls exactly in the center of a group of numbers after they have been sorted into order is known as the median. (Note the number is not always the mid-value; it will just be halfway into the set.)

The number or numbers that repeat the most frequently in a group of numbers is called the mode. 

Probability rules and counting principles

The area of mathematics known as probability gives us the capacity to measure uncertainty and forecast the possibility that particular events will occur.

An event is a set of outcomes. An outcome is the result of an experiment. A sample space is the set of all experimental outcomes.

For example, if we flip a coin, the sample space comprises two possible outcomes heads or tails. There are six possible outcomes in the sample space if we roll a die 1, 2, 3, 4, 5, or 6.

The probability of an event is a number between 0 and 1, inclusive, that expresses the possibility that the event will occur. If an occurrence is impossible, it has a probability of 0. If an event is certain, then its probability is one. For instance, with a regular die, the likelihood of rolling a seven is zero, and the likelihood of rolling a number lower than seven is one.

The counting principle refers to a set of criteria for counting the number of possible outcomes in a sample space.

1. Permutations A permutation is an arrangement of objects in a certain order. The number of permutations of n items taken r at a time is indicated by P(n, r), which is provided by

P(n,r)= n!/(n-r)!

Here, n! represents the factorial of n, which is the product of all positive integers up to and including n.

2. Combinations 

A combination is a group of items where the arrangement is unimportant. The number of combinations of n objects taken r at a time, denoted by C(n, r), is given by

c(n,r)= n! /(r!*(n-r)!) 

3. Binomial Coefficient

The binomial coefficient is a number that shows the number of possibilities to select r things from n objects. With the notation C(n, r), the binomial coefficient is represented as follows

c(n,r)= n! /(r!*(n-r)!) 

Trigonometry 

The provided subsections outline the key areas of trigonometry tested on the SAT

 Understanding Sine, Cosine, and Tangent

Although trigonometry makes up less than 5% of all math questions, you still want to get those questions right, and you won’t be able to answer any trigonometry questions correctly without knowing the following formulas

sin(x)= Measure of the opposite side to the angle/Measure of the hypotenuse 

Cos (x)= Measure of the adjacent side to the angle/Measure of the hypotenuse

Tan(x)= Measure of the opposite to the angle/Measure of the adjacent side to the angle

Example-

Sin (x) = 9/15= 0.6

Cos (x)= 12/15= 0.8

Tan (x)= 9/12=0.75

 Special Triangles and their formulas 

On the SAT, two main types of special triangles are frequently encountered

1. 30-60-90 Triangles

• Properties
  • Each angle measures 30°, 60°, and 90°.
  • The sides are proportional to 1√32, where the shortest side is opposite the 30° angle, the longer leg is opposite the 60° angle, and the hypotenuse is the longest side.
  • Trigonometric ratios for these angles are easily memorized
    • sin(30°) = 1/2
    • cos(30°) = √3/2
    • tan(30°) = 1/√3
    • sin(60°) = √3/2
    • cos(60°) = 1/2
    • tan(60°) = √3

2. 45-45-90 Triangles

• Properties
  • Each angle measures 45°, 45°, and 90°.
  • The sides are all proportional to 11√2, where all sides are the same length.
  • Trigonometric ratios for the 45° and 90° angles are readily available
    • sin(45°) = cos(45°) = √2/2
    • tan(45°) = 1

Utilizing these special triangles on the SAT

• Recognizing a triangle as a 30-60-90 or 45-45-90 triangle allows you to apply the memorized properties and ratios directly to solve for missing side lengths or angles without complex calculations.
• This can significantly save time and effort compared to using trigonometric formulas from scratch, especially when dealing with basic problems.

 Radians and Degrees

Radians and degrees are both units used to measure angles, but they represent different concepts. Understanding the relationship between them is crucial for solving trigonometry problems on the SAT.

Degrees

• The most familiar unit for measuring angles is divided into 360°.
• A full circle is considered 360°.
• Used in everyday life and most graphical representations of angles.

Radians

• Less common unit, based on the ratio of the arc length to the radius of a circle.
• One radian is the angle formed when the arc length is equal to the radius of the circle.
• A full circle is equal to 2π radians (π being a mathematical constant approximately equal to 3.14).

Conversion between Radians and Degrees

• The SAT formula sheet typically provides the conversion formula
  • 1 radian = 180°/π
  • 1 degree = π/180 radians

Importance for SAT Math

• While the SAT primarily uses degrees, understanding radians can be crucial in certain situations
  • Trigonometric tables or calculators might provide values in radians.
  • Some problems might involve converting between degrees and radians before using trigonometric functions.

Advanced Math Topics 

While the SAT math section primarily focuses on core algebraic and geometric concepts, exploring advanced topics like complex numbers, polynomial division, and non-linear functions can offer a strategic advantage in your preparation. 

Complex numbers

The addition of a real number and an imaginary number is known as a complex number.

Example- 5+i

 Polynomial division

An algebraic expression with more than two terms, typically of similar bases and distinct powers, is called a polynomial. Integer terms are often included in polynomials.

When dividing polynomials, it is critical to find similar bases and apply the rule of exponents to simplify variable-containing components.

Example- 

 Non-linear functions and their graphs

As the name implies, a nonlinear function is not linear. Stated otherwise, a nonlinear function’s graph is NOT a line. That is to say, its graph need not be a straight line.

Example- 

SAT Math Formula Sheet

The SAT math formula sheet plays a crucial role in your test-taking strategy. Here’s a breakdown of the provided subsections to help you make the most of it

 Compilation of Essential Formulas

The figure below shows the formula box you will receive for each math section on the SAT.

It’s essential to familiarize yourself with these formulas before the test and understand the situations where each formula applies.

How to Effectively Use a Formula Sheet?

• This subsection likely offers guidance on strategically utilizing the formula sheet during the SAT
  • Identify relevant formulas Quickly scan the sheet to find the formulas applicable to the specific problem you’re tackling.
  • Understand the notation Ensure you comprehend the symbols and variables used in each formula.
  • Plug in values Substitute the given values from the problem into the appropriate formula.
  • Simplify and interpret Calculate the answer and interpret the result in the context of the problem.
• Remember, the formula sheet is a reference tool, not a crutch. Aim to understand the underlying concepts behind the formulas, not just memorize them mechanically.

Customizing Your Formula Sheet for Quick Reference

• This subsection might suggest strategies for personalizing your formula sheet to enhance its effectiveness
  • Organize formulas logically Group related formulas together for easier retrieval.
  • Highlight key information Emphasize frequently used formulas or specific parts within formulas for quick reference.
  • Add personal notes Include brief explanations or reminders to aid your understanding.

Test-Taking Strategies and Tips

Acing the SAT math exam with solid knowledge of the SAT math formula is backed by effective test-taking strategies. Here’s a breakdown of the provided subsections to equip you with the tools you need for success

Time Management on the SAT Math Section

• Plan your approach Divide the allocated time strategically based on the number of questions and their difficulty levels.
• Prioritize effectively Focus on completing easier questions first to build confidence and avoid getting bogged down on challenging problems.
• Manage your pace Allocate sufficient time for reviewing your answers, especially toward the end of the section.
• Practice with timed conditions Simulate the actual test environment by taking practice tests under time constraints to develop your time management skills.

Guessing Strategies and When to Skip Questions

• There is no penalty for guessing on the SAT. Even if you’re unsure of the answer, it’s always better to make an educated guess than leave a question blank.
• Eliminate answer choices you know are incorrect. This can significantly increase your chances of guessing correctly among the remaining options.
• Use logical reasoning to narrow down your choices. Consider the context of the problem and the properties involved to eliminate implausible options.
• Learn to identify when to skip a question if you’re completely stuck and have no clue how to approach a problem, move on, and revisit it later if time permits. Focus on maximizing your points on questions you have a better chance of answering correctly.

Practice Tests and Review Techniques

• Regularly take practice tests under timed conditions to simulate the actual SAT experience and identify areas needing improvement.
• Thoroughly review your practice tests Analyze your mistakes, understand why you got them wrong, and learn from them to avoid repeating the same errors.
• Focus on understanding the concepts behind the problems, not just memorizing solutions. This will equip you to tackle similar problems with different approaches and variations.
• Seek help from teachers, tutors, or online resources if you encounter particular concepts or problems you struggle with.

Beyond the Basics Master SAT Math Formulas with LearnQ.ai

In this guide, we tried to give a complete overview of all the important SAT math formulas, but if you want to deepen your knowledge, and sharpen your skills, we would recommend you leverage the learnQ.ai platform. 

Tired of memorizing dry formulas for the SAT? LearnQ.ai, a leader in AI-powered SAT prep, understands the struggle. We offer a complete learning suite that goes beyond formulas and makes mastering the SAT fun and effective.

Here’s what students love about LearnQ.ai

• Playful Learning Master concepts and strategies through engaging exercises and games, making studying less like a chore and more like a fun challenge.
• Your AI Study Buddy, Mia Need help with a tricky question? Mia, our friendly AI assistant, is always there to answer your questions and guide you through challenging topics.
• Fresh Content, Always Never run out of practice! We offer a massive library of fresh, high-quality questions to keep your learning dynamic and engaging.
• Personalized Insights Gain valuable data-driven insights into your strengths and weaknesses, allowing you to focus your efforts on areas that need the most improvement.

In essence, LearnQ.ai simplifies the journey to excelling in SAT math formulas by leveraging the power of AI technology, making learning personalized, adaptive, and insightful. 

Ready to take your SAT prep to the next level? Visit LearnQ.ai today and experience the future of learning!

Conclusion

Mastering SAT math formulas and strategies is the key to exam success. With LearnQ.ai’s innovative AI-powered platform, you can make formula memorization engaging and effective.

Gain personalized insights, access a vast question bank, and learn through interactive exercises designed for maximum retention and real-world application. Unlock your full potential with LearnQ.ai today.