Making Math Fun: Transforming Your SAT Prep Experience
Let’s be real — math isn’t everyone’s favorite subject. In fact, for many students, math can seem downright uninteresting and daunting.
But here’s the deal: math is a crucial part of the SAT, and doing well in this section can significantly boost your overall score. It’s about logical thinking and analytical skills that are vital in college and beyond.
Now, what if we told you there’s a way to make SAT math subjects more engaging, even fun? Enter gamified prep methods.
Ready to change your perspective on math and ace the SAT? Let’s dive into the SAT math subjects in detail along with some gamified strategies that will make your prep sessions something to look forward to!
Trust us and team up with LearnQ.ai to crush the SAT math section! With awesome study resources, practice tests, and more, you’ll be ready to tackle any math challenge.
Gamified Prep Methods for SAT Math Subjects — Key Highlights
Gamified prep methods for digital SAT bring a whole new level of engagement and effectiveness to your study routine.
Think of turning your SAT math subject practice into a game where you earn points, unlock levels, and maybe even compete with friends. These methods benefit you by making study sessions more enjoyable and motivating through reward systems.
Through gamified learning, you can benefit from the following:
Transform studying from a chore into an exciting challenge
Easily stay motivated and retain information
Enhance your study routine and make tricky math problems less intimidating
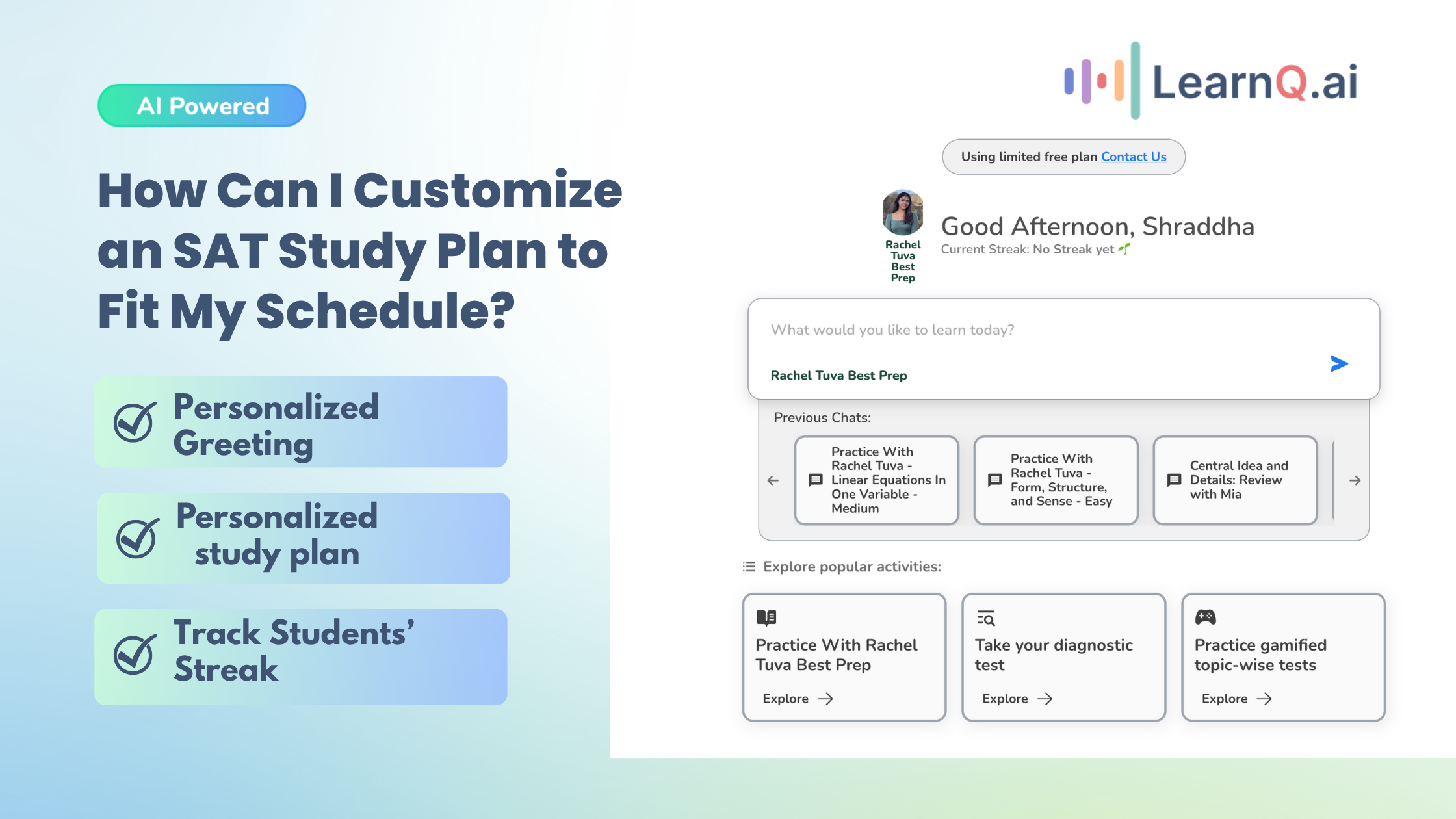
Introducing LearnQ’s AI-Driven Gamified SAT Preparation Platform
LearnQ’s gamified interactive apps and platforms take this concept to the next level. You’ll find yourself immersed in online games and quizzes designed specifically to help you master SAT concepts while having fun.
Whether it’s tackling math problems or refining your reading skills, these interactive tools make learning interactive and enjoyable.
Plus, with “Ask Mia,” our AI tutor available 24/7, you can get instant help whenever you’re stuck, making your SAT prep journey smoother and more effective than ever before.
Step-by-Step Guide to Master SAT Math Problems
Now let’s get you started with LearnQ’s Play and Practice section, where you can practice relevant questions and master multiple math concepts.
Here’s a step-by-step guide to help you excel in the Math “Problem Solving & Data Analytics” section that will help you build a strong foundation and develop effective problem-solving skills.
Step 1: Familiarize Yourself with LearnQ
Explore the features and interface of LearnQ to understand how to navigate through the tool.
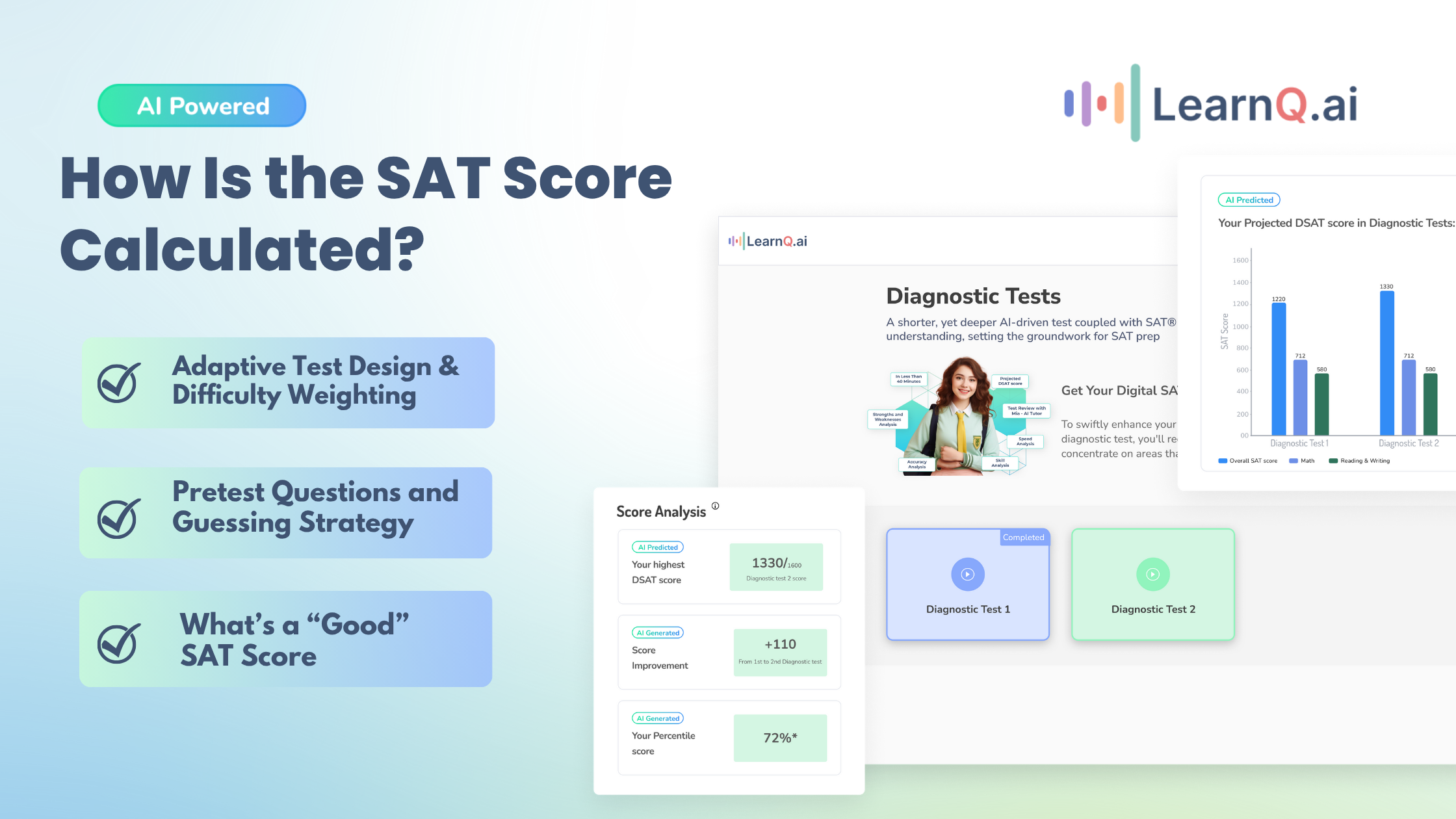
Step 2: Assessment and Goal Setting
Take an initial assessment test on LearnQ to gauge your current proficiency level in Math Problem Solving & Data Analytics.
Set specific, measurable goals based on your assessment results, such as improving accuracy in probability calculations or enhancing data interpretation skills.
Step 3: Topic Selection and Learning Paths
Identify key areas within Math Problem Solving & Data Analytics that you want to focus on, such as ratios, rates, proportions, percentages, and probability, or data analysis.
Follow step-by-step instructions within each module to understand concepts and rules thoroughly.
Step 4: Practice and Application
Practice solving a variety of problems and data analysis exercises available on LearnQ.
Apply learned concepts to real-world scenarios presented in the tool’s case studies or practical examples.
Once you click ‘play now’, you’ll navigate to the SAT math probability questions on the LearnQ website.
Also Read: Digital SAT Practice Questions & Resources
Math Question Types on the Digital SAT at a Glance
To apply such gaming prep strategies for clearing math problems, have no doubts in SAT math subjects and syllabus.
The math section has a total of 44 questions to be answered in 70 minutes. Approximately 75% of SAT Math questions are multiple-choice, with the remaining 25% requiring free-response numerical answers. The order of topics covered can vary between tests.
The math section on the digital SAT is divided into four domains as follows:
Content domain | Percentage of Questions Appeared So Far | Number of Questions |
Algebra | 35% | 13–14 |
Advanced Math | 35% | 13–15 |
Problem Solving and Data Analysis | 15% | 5–7 |
Geometry and Trigonometry | 15% | 5–7 |
LearnQ.ai is Powered by VEGA AI—Is your Institute Next?
Give students a Duolingo-style test-prep platform with Shopify-level customization for tutors and institutes.
Concepts Covered on the Math Section of the Digital SAT
Algebra
Linear equations and inequalities form a fundamental part of SAT Math subjects. These problems require you to solve for a variable or analyze the relationship between variables.
Algebra includes the following types of questions:
- Linear equations in 1 variable
- Linear equations in 2 variables
- Linear functions
- Systems of 2 linear equations in 2 variables
- Linear inequalities in 1 or 2 variables
You’ll need to be comfortable with manipulating equations, understanding slope and intercept, and graphing linear relationships.
Problem 1:
Solve for x in the equation: 3x − 5 = 10
Options:
- 2
B. 5
C. 15/3
D. 5/3
Correct answer: B. 5
Explanation:
To solve 3x − 5 = 10: 3x = 10 + 5
3x = 15
x = 5
- 2
Problem 2:
Graph the inequality: 2x + 3y ≤ 6
Options:
- A line through (0, 2) and (3, 0) shaded below
B. A line through (0, 3) and (2, 0) shaded above
C. A line through (0, 2) and (3, 0) shaded above
D. A line through (0, 3) and (2, 0) shaded below
Correct answer: A. A line through (0, 2) and (3, 0) shaded below
Explanation:
To graph 2x + 3y ≤ 6, first rewrite the equation in slope-intercept form.
3y ≤ −2x + 6
Y ≤ −2/3x + 2
The line passes through (0, 2) and (3, 0) and is shaded below because of the ≤ inequality.
- A line through (0, 2) and (3, 0) shaded below
Advanced Math
In the Advanced Math section of the SAT, you’ll be tackling a variety of complex mathematical concepts. This includes solving and analyzing equivalent expressions, as well as nonlinear equations in one variable and systems of nonlinear equations.
Nonlinear functions can be one of the following types:
- Quadratic
- Polynomial
- Exponential
- Absolute value
- Rational
- Radical
The types of questions that usually appear in this section are:
- Equivalent expressions
- Nonlinear equations in 1 variable
- Systems of equations in 2 variables
- Nonlinear functions
Problem 1:
Solve the quadratic equation: x2 − 4x − 5 = 0
Options:
- x = 1 or x = −5
B. x = −1 or x = 5
C. x = 1 or x = 5
D. x = −1 or x = −5
Correct answer: B. x = −1 or x = 5
Explanation:
To solve the quadratic equation x2 − 4x − 5 = 0, factorize it.
(x − 5)(x + 1) = 0
Set each factor equal to zero: x − 5 = 0 ⇒ x = 5
x + 1 = 0 ⇒ x = −1
So, the right answer is option B.
- x = 1 or x = −5
Problem Solving and Data Analysis
Problem-solving and Data Analysis focuses on your ability to use quantitative reasoning to tackle problems involving ratios, rates, and proportional relationships. It also assesses your understanding and application of unit rates and your ability to analyze and interpret data involving one or two variables.
These skills are essential for developing quantitative literacy, which is crucial not only for college courses and career training programs but also for navigating everyday life.
Problem-Solving and Data Analysis includes the following skills and knowledge testing points:
- Ratios, rates, proportional relationships, and units
- Percentages
- One-variable data: distributions and measures of center and spread
- Two-variable data: models and scatter plots
- Probability and conditional probability
- Inference from sample statistics and margin of error
- Evaluating statistical claims: observational studies and experiments
Let’s look at a few samples of different concepts for better understanding.
Problem 1: Ratios and proportions
A car travels 150 miles using 5 gallons of gasoline. What is the car’s fuel efficiency in miles per gallon?
Options:
- 25 miles per gallon
B. 30 miles per gallon
C. 35 miles per gallon
D. 20 miles per gallon
Correct Answer: B. 30 miles per gallon
Explanation: To find the car’s fuel efficiency:
Fuel Efficiency = Miles/Gallons = 150/5 = 30
- 25 miles per gallon
Enhance your Digital SAT study routine with AI-driven insights and personalized practice tests.
Problem 2: Percentages
The table below shows the number of students who prefer different types of extracurricular activities at a high school.
Activity
Number of Students
Sports
120
Music
80
Art
50
Science Club
30
Drama
20
What percentage of students prefer Music?
What percentage of students prefer Music?
Options:
- 20%
B. 25%
C. 30%
D. 40%
Correct Answer: B. 25%
Explanation:
First, find the total number of students:
120 + 80 + 50 + 30 + 20 = 300
Next, calculate the percentage of students who prefer Music:
80/300 × 100 = 8000/300 ≈ 26.67%
So, the answer is option B.
Problem 3: Probability
In a survey, 300 students were asked about their favorite types of music and whether they prefer to listen to it on streaming platforms or CDs. The results are summarized in the table below:
Favorite Music Type
Streaming
CDs
Pop
120
40
Rock
80
60
Hip Hop
100
20
Total
300
120
If a student is randomly selected from this group, what is the probability that the student prefers Pop music given that they listen to it on CDs?
Options:
- A) 1/3
- B) 1/4
- C) 1/2
- D) 2/3
- E) 3/4
Correct Answer: B) 1/4
Explanation:
To find the probability of a student preferring Pop music, we use the formula for conditional probability:
P(Pop | CDs) = P (Pop and CDs) / P (CDs) |
From the table:
- Number of students who prefer Pop music and listen to it on CDs = 40
- Total number of students who listen to CDs = 120
So, P(Pop | CDs) = 40/120 = 1/3
Therefore, the probability that a student prefers Pop music given that they listen to it on CDs is 1/3.
Problem 4: Statistics and Margin of Error
A researcher surveyed a random sample of 200 students from a high school to determine the average number of hours spent on homework per week. The sample mean was found to be 15 hours, with a margin of error of ±2 hours.
Which of the following is the best interpretation of the margin of error in this context?
Options:
- The true average number of hours spent on homework per week for all students at the high school is exactly 15 hours.
B. The true average number of hours spent on homework per week for all students at the high school is between 13 and 17 hours.
C. The sample mean could be 2 hours more or less than the actual time spent on homework per week by the surveyed students.
D. The survey results are accurate for only the 200 students who were surveyed.
Correct Answer: B. 13 and 17 hours
Explanation:
The margin of error indicates the range within which the true average number of hours spent on homework per week for the entire student population is likely to fall.
Given:
- Sample mean (x̄) = 15 hours
- Margin of error = ±2 hours
The formula to calculate the confidence interval is:
Confidence Interval = x̄ ± Margin of Error
Substitute the values: Confidence Interval = 15 ± 2
Calculate both ends of the interval:
- Lower bound = 15 − 2 = 13 hours
- Upper bound = 15 + 2 = 17 hours
Therefore, the true average number of hours spent on homework per week is likely between 13 and 17 hours.

Geometry and Trigonometry
Geometry and Trigonometry measure the ability to solve problems that focus on the following:
- Area and volume
- Lines, angles, and triangles
- Right triangles and trigonometry
- Circles
Problem 1
In triangle ABC, ∠ABC = 90° and AB = 5 units. If AC = 7 units, what is the length of BC?
Options:
- 12 units
- 10 units
- 8 units
- 4 units
Correct Answer: D. 4 units
Explanation:
Since ∠ABC = 90°, triangle ABC is a right triangle with AB as one leg and AC as the hypotenuse.
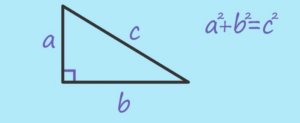
To find BC, use the Pythagorean theorem: BC = sqrt {AC2 − AB2}
BC = sqrt {72 − 52}
BC = sqrt {49 – 25}
BC = sqrt {24}
BC = sqrt{4 × 6}
BC =2 sqrt{6}
Therefore, the length of BC ≈ 4.9 units
Problem 2
What is the area of a circle with radius r = 6 units?
Options:
- 36π square units
- 18π square units
- 12π square units
- 9π square units
Correct Answer: A. 36π square units
Explanation:
The area of a circle is given by the formula: A= πr2
Substitute r = 6: A = π × 62 = 36π
Therefore, the area of the circle is 36π square units, which corresponds to option A.
Please Note: The aforementioned examples illustrate the types of problems you might observe in SAT math subjects, which require you to apply quantitative reasoning to real-world scenarios.
LearnQ.ai is powered by VEGA AI—Is your institute next?
Offer students a Duolingo-style test-prep platform with Shopify-level customization for tutors and institutes.





Conclusion
Having grasped the syllabus of SAT math subjects, if you grasp the right techniques, they become much simpler.
Understanding the basics and practicing different question types builds confidence. Take time to analyze mistakes for better understanding. Repetition and exposure to various problems are key to mastering probability on the SAT.
Utilize the wealth of SAT prep materials available for targeted practice. Keep pushing forward, review diligently, and leverage all resources at your disposal. You’re well on your way to mastering the SAT!
Master your math skills and excel in all areas of the digital SAT with LearnQ’s Diagnostic Test! In just 40 minutes, you’ll uncover your strengths, pinpoint areas for improvement, and get on the fast track to acing the exam.