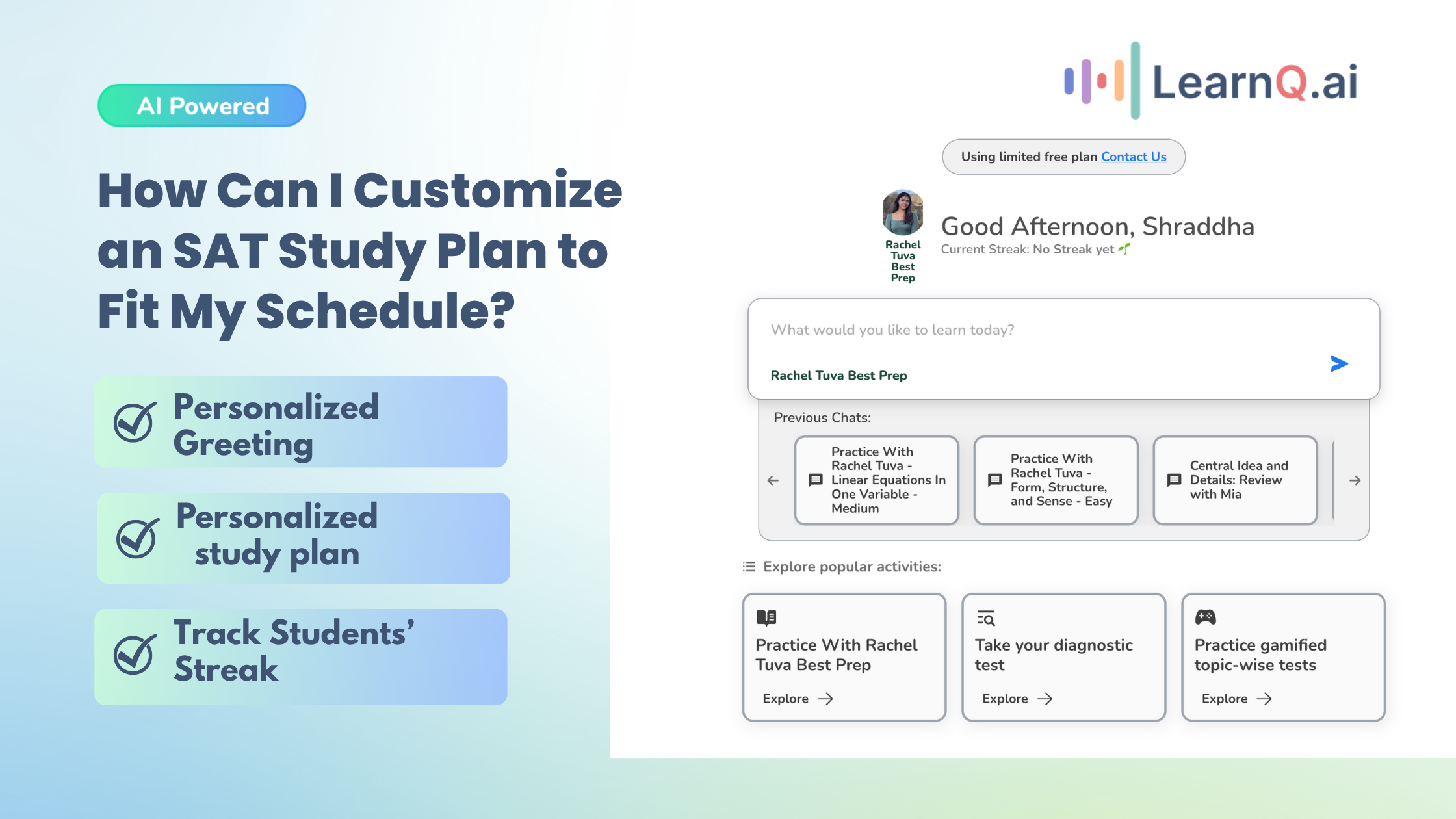
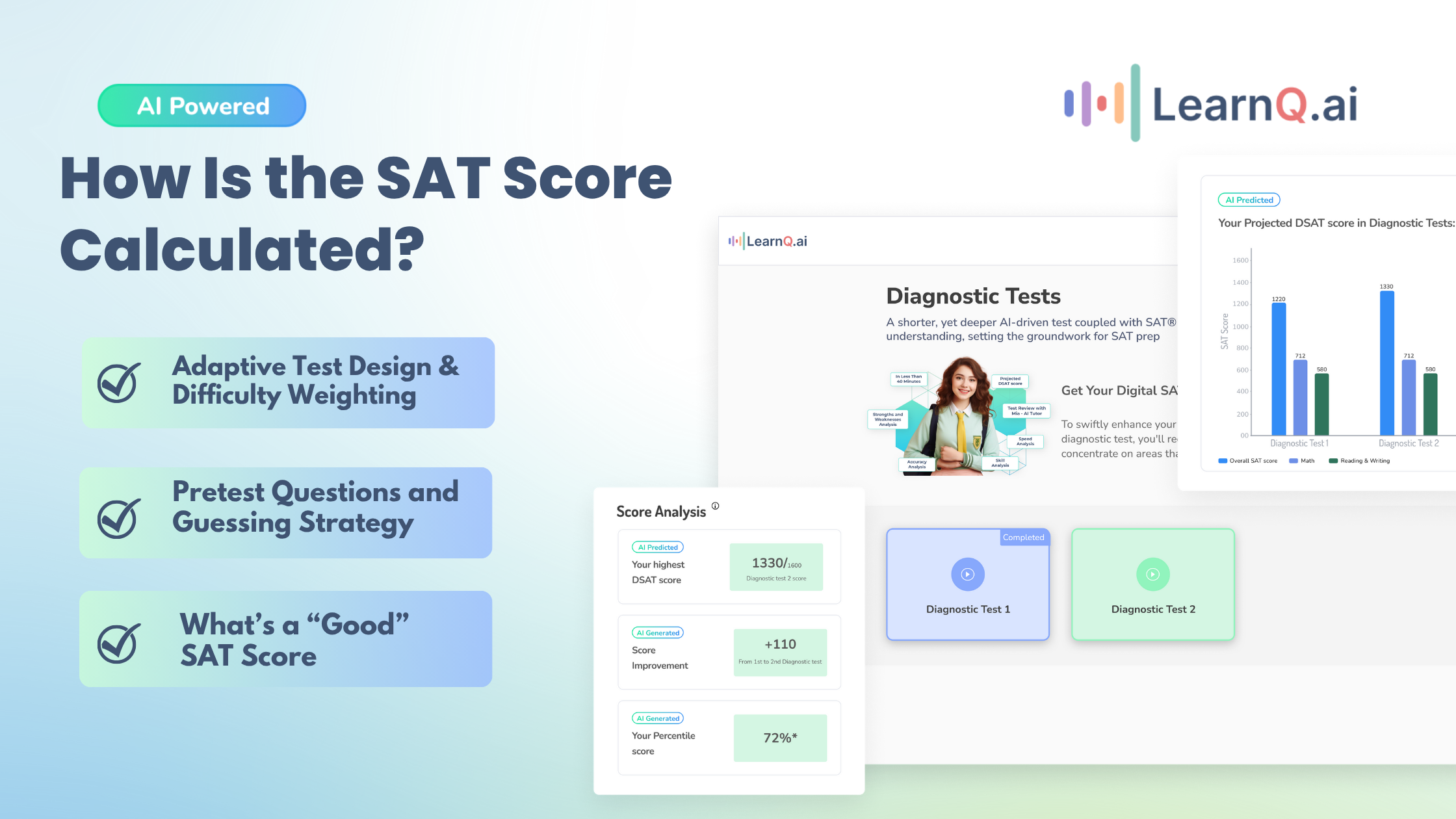
Mastering SAT Circle Problems
Are you an SAT warrior who is ready to tackle the circle problems that pop up on the SAT Math Test?
Circles are a fundamental geometric shape, but on the SAT, they can turn into tricky problems that throw your score off track. Whether it’s finding the area of a shaded region or figuring out the length of an arc, learning these round riddles can seriously boost your score.
So, grab your compass (just kidding, you won’t need one!), and let’s learn about digital SAT Math circle questions! Remember you’re not going at it alone! LearnQ.ai is your reliable digital SAT prep partner, here to supercharge your test success.
Topics Covered in Digital SAT Math Circles Questions
On the SAT Math Test, circle problems are part of the larger geometry and trigonometry content area. Here’s what you typically need to know:
- Basic Properties: Understand the parts of a circle including radius, diameter, circumference, and area.
- Equations: Be comfortable with the standard equation of a circle in the coordinate plane.
- Arcs and Angles: Know how to calculate the measures of arcs and angles in and around circles, including central angles, inscribed angles, and angles formed by tangents and chords.
- Sector Area and Arc Length: Be able to find the area of a sector and the length of an arc, essential for solving more complex problems involving parts of circles.
- Chords, Secants, and Tangents: Solve problems involving the properties of chords, secants, and tangents, including the relationships and theorems associated with them.
This coverage ensures that you can face a variety of questions on test day, from straightforward calculations to more intricate problems that require deeper reasoning.
Remember, every point counts, so make those circle questions fear your newfound skills!
Understanding Basic Circle Concepts
Alright, now let’s get you prepped for solving SAT Math circle questions! From the very basics to those tricky relationships and formulas, here’s everything you need to know about circles.
1. Properties of Circles
Imagine a point in space, and then imagine all the points that are exactly the same distance from that central point. What path do those points make? That’s your circle!
- The distance from the center to any point on the circle is called the radius. Double the radius and you’ve got the diameter, which stretches across the circle through the center. The outer edge of the circle, the path itself, is known as the circumference.
- Another cool thing about circles is their symmetry. They are perfectly symmetrical in their diameter and about any line through the center, making them unique among shapes.
2. Formulas for SAT Math Circles Questions
To tackle circle problems effectively, you’ll need to have some key formulas at your fingertips:
Circumference: 𝐶 = 2𝜋𝑟 or 𝐶 = 𝜋𝑑, where 𝑟 is the radius and 𝑑 is the diameter
Area: 𝐴 = 𝜋r2, which gives you the space inside the circle
While these formulas are your bread and butter for solving most of the SAT Math circles questions, understand how the radius, diameter, and circumference are intimately connected.
Radius: Half the length of the diameter
Diameter: Twice the length of the radius, or 𝑑 = 2𝑟
Circumference: If you think about wrapping a string around the circle and then measuring the string, you’d have the circumference.
Remember, 𝐶 = 𝜋𝑑 or 𝐶 = 2𝜋𝑟
So, this means the circumference is a little more than three times the diameter.
3. Significance of π in Circle Geometry
Pi (𝜋) is a mathematical constant that represents the ratio of any circle’s circumference to its diameter, approximately equal to 3.14159.
It’s a key player in circle geometry because it connects the linear dimensions of circles (like the radius and diameter) with the non-linear measurement (like area and circumference).
No matter how big or small the circle is, 𝜋 remains the same, making it one of the coolest and most mystical numbers in math!
For instance, if you have a circle with a radius of 4 units:
Circumference: 𝐶 = 2𝜋 (4) = 8𝜋 units
Area: 𝐴 = 𝜋(4)2 = 16𝜋 square units
Have trouble with complex SAT Math circle questions? Say hello to Mia — your friendly AI tutor at LearnQ! No matter the challenge or the topic, Mia is here to help.
Circle Equations and Their Applications
SAT Math circles questions might look a bit like a secret code at first, but once you crack them, a whole new realm of problem-solving opens up. Here’s how you can master these equations and apply them to those SAT questions.
Standard Equation of a Circle
The standard form of a circle equation is
(x−h)2 + (y−k)2 = r2 |
Here’s what each term represents:
- x and y are the coordinates of any point on the circle
- h and k are the coordinates of the center of the circle
- r is the radius of the circle
Question
You’re given a circle with the center at (3,−4) and a radius of 5. Find the equation of the circle.
Answer:
Take a look at the below image for Mia AI’s detailed solution.
Super straightforward, right?
LearnQ.ai is Powered by VEGA AI—Is your Institute Next?
Give students a Duolingo-style test-prep platform with Shopify-level customization for tutors and institutes.
2. How to Apply Circle Equations in SAT Problem Solving
Circle equations are super handy in solving a variety of SAT problems, especially those involving geometry in the coordinate plane. For instance, you might be asked to:
Find the radius or center of a circle given its equation.
Determine if a certain point lies on, inside, or outside the circle.
Calculate the intersection points of a circle with other shapes, like lines or other circles.
Question
You’re given the point (7,−1) and the circle equation (x−3)2 + (y+4)2 = 16. Find if the point is on the circle.
Options:
- A) Yes, the point lies on the circle.
- B) No, the point does not lie on the circle.
- C) The point lies inside the circle.
- D) The point lies outside the circle.
Correct Answer: B) No, the point does not lie on the circle.
Explanation:

3. Transforming and Interpreting Circle Equations
Sometimes, SAT problems give you a circle equation in a not-so-obvious format, and you might have to do a bit of algebra to get it into the standard form. This can involve completing the square, a method used to reformat quadratic expressions into a perfect square.
Question
Let’s say you have the equation x2 − 6x + y2 + 8y = −9, find the center and radius of the circle.
Options:
- A) Center: (−3,4), Radius: 3
B) Center: (3,−4), Radius: 4
C) Center: (3,−4), Radius: 5
D) Center: (−3,4), Radius: 5
Correct Answer: B) Center: (3,−4), Radius: 4
Explanation:
- A) Center: (−3,4), Radius: 3

With some practice and our Mia’s quick assistance, you’ll be able to handle these problems like a pro — just remember, it’s all about recognizing patterns and applying the right techniques!
Also read: Digital SAT Question Bank For Perfect Preparation
Step-by-Step Solutions for SAT Math Circles Questions
Let’s look at five example problems that demonstrate how to use circle equations and formulas effectively.
Example 1: Find the Radius
Question
Find the radius of the circle given by the equation (x−2)2 + (y+3)2 = 49
Options:
- A) 5
- B) 6
- C) 7
- D) 8
Correct Answer: C) 7
Explanation:

Therefore, the radius r = sqrt{49} = 7
Example 2: Determine the Center
Question
What is the center of the circle whose equation is (x+4)2 + (y−5)2 = 36?
Options:
- A) (4, -5)
- B) (-4, -5)
- C) (4, 5)
- D) (-4, 5)
Correct Answer: D) (-4, 5)
Explanation:
Look at the screenshot of the problem solved by Mia.

Example 3: Equation from Graph Details
Question
Write the equation of a circle with a center at (3,−3) and passing through (3,0)
Options:
- A) (x+3)2 + (y-3)2 = 9
- B) (x−3)2 + (y+3)2 = 9
- C) (x−3)2 + (y+3)2 = 3
- D) (x+3)2 + (y-3)2 = 3
Correct Answer: B) (x−3)2 + (y+3)2 = 9
Explanation:

Example 4: Point Inside or Outside
Question
For the circle (x−1)2 + (y−1)2 = 16, determine if the point (5,5) is inside, on, or outside the circle.
Options:
- A) Inside the circle
- B) On the circle
- C) Outside the circle
Correct Answer: C) Outside the circle
Explanation:

Example 5: Intersection with a Line
Question
Find if the line y = x + 2 intersects the circle x2+y2=20
Options:
- A) The line does not intersect the circle
- B) The line intersects the circle at one point
- C) The line intersects the circle at two points
- D) The line is tangent to the circle
Correct Answer: C) The line intersects the circle at two points
Explanation:

Solo educators or enterprise institutions are choosing LearnQ for SAT Math test preparation.
Want to know why? If your student’s actual digital SAT score falls short of the projected score from the initial diagnostic test on LearnQ.ai, we promise a full refund!
Typical SAT Math Circles Questions
As you had a glimpse at the examples of SAT Math circles questions, your confidence would’ve boosted for handling similar test questions. Now is the time to see some typical SAT circle problems, breaking them down step by step.
Example 1: Finding the Radius from a Chord
Question
In a circle, a chord that is 8 cm long is 6 cm from the center of the circle. Find the radius of the circle.
Options:
- A) sqrt{50} cm
- B) sqrt{36} cm
- C) sqrt{48} cm
- D) sqrt{52} cm
Correct Answer: D) sqrt{52} cm
Explanation:

This approach demonstrates how to leverage geometry, specifically the Pythagorean theorem, to solve problems involving circles on the SAT.
Enhance your Digital SAT study routine with AI-driven insights and personalized practice tests.
Example 2: Intersection of a Circle and a Line
Question
A line with the equation y=2x+3 intersects a circle with the equation (x−1)2 + (y−2)2 = 25 at points A and B. Find the coordinates of points A and B.
Options:
- A) (1, 5) and (5, 13)
- B) (-3, -3) and (5, 13)
- C) (-3, -3) and (3, 9)
- D) (1, 1) and (5, 13)
Correct Answer: B) (-3, -3) and (5, 13)
Explanation:

Verify the Points:
For x = -3:
y = 2(−3) + 3 = −6 + 3 = −3
For x = 5:
y = 2(5) + 3 = 10 + 3 = 13
Thus, the points of intersection are (-3, -3) and (5, 13)
Example 3: Circumference and Area Comparison
Question
Two circles have radii of 7 cm and 10 cm, respectively. How much longer is the circumference of the larger circle compared to the smaller one, and how much greater is its area?
Options: A) Circumference: 4π cm, Area: 48π cm2
B) Circumference: 6π cm, Area: 51π cm2
C) Circumference: 8π cm, Area: 56π cm2
D) Circumference: 10π cm, Area: 60π cm2Correct Answer: B) Circumference: 6π cm, Area: 51π cm2
Explanation:
Let’s calculate the circumferences.
Circumference of the smaller circle:
C1 = 2π (7) = 14π cm
Circumference of the larger circle:
C2 = 2π (10) = 20π cm
Difference in circumference: 20π − 14π = 6π cm
Now, calculate the areas:
Area of smaller circle:
A1 = π (72) = 49π cm2
Area of larger circle:
A2 = π (102) = 100π cm2
Difference in area: 100π − 49π = 51π cm2
So, the circumference of the larger circle is 6π cm longer than that of the smaller circle.
And, the area of the larger circle is 51π square cm greater than that of the smaller circle.
Tangency-Related SAT Math Circles Questions
Tangency is a fundamental concept in circle geometry, referring to the point where a line or another circle just touches the circle without crossing it.
When two circles are tangent to each other, they touch at exactly one point.
This scenario can give rise to various problems, such as finding the:
- Distance between the centers of the circles or solving for unknown radii
- Point of tangency to a circle from a point outside is perpendicular to the radius
Here are two SAT-style problems that involve the concept of tangency and circles being tangent to one another:
Problem 1: Finding the Distance Between Centers
Question
Two circles are tangent to each other externally at point T. The radius of the first circle is 3 cm, and the radius of the second circle is 5 cm. What is the distance between the centers of these two circles?
Options:
- A) 2 cm
B) 5 cm
C) 8 cm
D) 10 cm
Correct Answer: C) 8 cm
Explanation:
- A) 2 cm
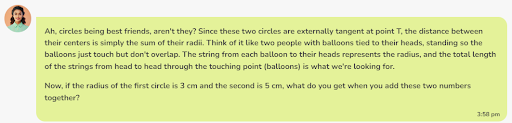
So, the distance between the centers of the two circles is 8 cm.
Problem 2: Finding the Radius of a Circle Tangent to Another Circle Inside a Rectangle
Question
A rectangle has dimensions 8 cm by 6 cm. A circle with a radius of 2 cm is tangent to one of the longer sides of the rectangle and one of the shorter sides. Another circle is tangent to the opposite sides of the rectangle and externally tangent to the first circle. Find the radius of the second circle.
Options:
- A) 1 cm
B) 2 cm
C) 3 cm
D) 4 cm
Correct Answer: C) 3 cm
Explanation:
- A) 1 cm

So, the radius of the second circle is 3 cm.

Converting Between Degrees and Radians
Understanding how to convert between degrees and radians is crucial, not just for circle-related problems but for trigonometry on the SAT in general. The key conversion factors to remember are:
180∘ is equivalent to π radians
To convert from degrees to radians, multiply by π / 180∘
To convert from radians to degrees, multiply by 180∘ / π
For example, converting 90° to radians:
90∘ × 180∘ / π = 2π radians
And converting π/4 radians to degrees:
π/4 radians × 180∘ / π = 45∘
Also Read: Digital SAT Practice Questions & Resources
Arcs and Angles in SAT Math Circles Questions
Arcs and angles — some of the coolest parts of circle geometry. They’re super useful for a ton of problems, and once you get the hang of them, you’ll be slicing through SAT questions like a hot knife through butter!
1. Formulas for Calculating Arc Lengths and Areas of Arc Sectors
When it comes to circles, not only do you need to worry about the whole pie, but sometimes just a slice of it as well. That’s where understanding arc lengths and sector areas comes in handy.
Arc Length: Think of this as the distance you’d travel if you were walking along the edge of a circle from one point to another. The formula is pretty straightforward:
Arc Length = Central Angle (in radians) × Circumference of the Circle = θ×r 2π |
where θ is the central angle in radians and r is the radius of the circle.
Example: If your circle has a radius of 5 meters, and your arc has a central angle of π/2 radians, the arc length would be: π/2 × 5 = 2.5π meters
Area of an Arc Sector: This is like finding the area of a pizza slice. Here’s how you calculate it:
Area of Sector = Central Angle (in radians) × Area of Circle = θ/2 × r2 2π |
Example: Using the same circle and angle as above, the sector area would be:
(π/2)/2 ×25 = 25π/4 square meters
2. Relationship Between Angles and Arcs in Circle Geometry
Let’s know the fundamentals of how angles and arcs relate to each other in a circle!
Central Angles and Arcs:
The central angle is simply the angle formed at the center of the circle by two radii drawn to the endpoints of the arc. The cool thing is that the measure of the central angle in degrees is exactly equal to the degree measure of the arc it intercepts.
Inscribed Angles and Their Arcs:
An inscribed angle is formed by two chords in a circle that meet at a point on the circle. The key thing to remember here is that the measure of an inscribed angle is half the measure of the arc it intercepts. So if you have an arc measuring 80 degrees, the inscribed angle cutting off that arc will measure 40 degrees.
Example: Imagine a circle where there’s a 120-degree arc.
An angle inscribed in that arc would measure: 120 / 2 = 60 degrees
LearnQ.ai is powered by VEGA AI—Is your institute next?
Offer students a Duolingo-style test-prep platform with Shopify-level customization for tutors and institutes.





Conclusion
You’ve made it through the maze of circle problems on the SAT! Take a quick rundown to ensure you’re fully prepped and ready to circle back to these questions with confidence.
- Keep essential formulas for circumference, area, arc length, and sector area at your fingertips. Remembering the properties of tangents, secants, and their angles can turn a tricky problem into a manageable one.
- Whether you’ve got a diagram or just a bunch of numbers and letters on the page, use your geometric intuition. Visualize the scenario if no diagram is provided, and always sketch one to help organize your thoughts if it helps.
- Keep a steady pace, especially in the no-calculator section. Practice with a timer to get a good feel for how long you can afford to spend on each question. Remember, not every circle problem needs to be solved to the last decimal—sometimes an estimate is enough to choose the right answer.
- Don’t just stick with what you have; explore online resources, SAT prep books, or educational apps. LearnQ offers tons of practice materials that are worth checking out.
- Reviewing what you got wrong is just as important as practicing what you can do right. Each mistake is a learning opportunity and understanding why you missed a question can prevent future errors.
Now that you’re armed with strategies and insights, go ahead and tackle those circle questions with the cool confidence of a geometry wizard.
While circle problems might look complicated at first, they are all about knowing your way around these basic relationships. Learn circle concepts and ace the digital SAT with LearnQ’s Diagnostic Test! In just 40 minutes, you’ll be all set for the SAT Math Test!