The digital SAT Math section has been redesigned to provide a better experience. You can now expect interactive question types and a greater emphasis on real-world applications.
Furthermore, the 2023 digital SAT Math has introduced new challenges as well. You need top-notch materials to practice for the hardest sat math question. Rigorous practice helps build the skills to tackle complex problems and improves test performance.
This blog will comprehensively guide you in mastering the hardest SAT Math questions, including 15 challenging practice problems with detailed step-by-step explanations.
Overview of Digital SAT Math Paper
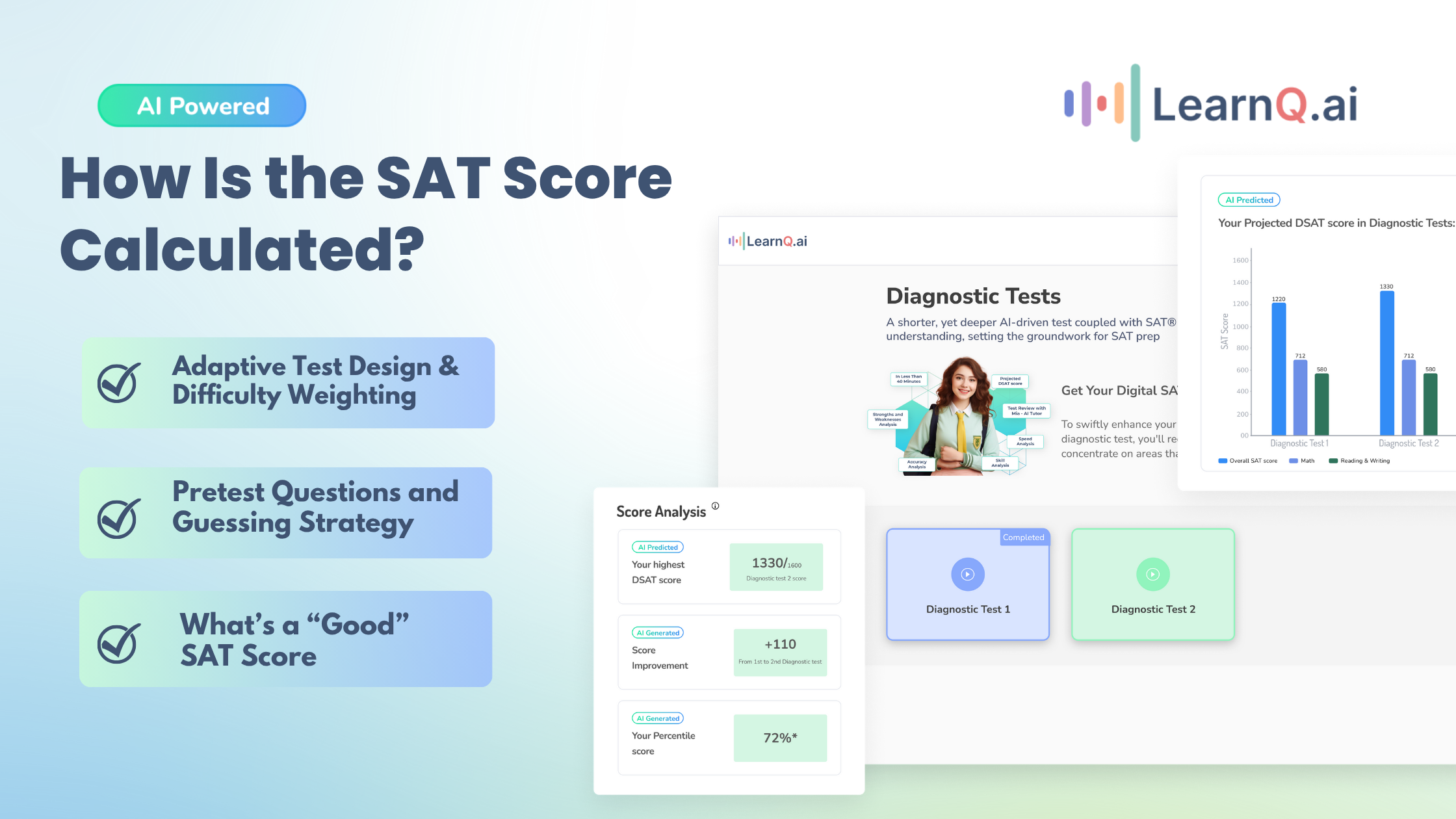
The digital SAT Math section is composed of 44 questions, split into 33 MCQs and 11 student-generated questions. You can use a calculator throughout the exam. The question distribution is as follows:
Category | Description | Percentage of Test |
Heart of Algebra | Linear equations and inequalities, their graphs, and systems. | 33% |
Problem Solving and Data Analysis | Ratios, proportions, percentages, units, analyzing graphical data, probabilities, and statistics. | 29% |
Passport to Advanced Math | Identifying and creating equivalent expressions, quadratic and nonlinear equations/functions, and graphs. | 28% |
Additional Topics in Math | Geometry, trigonometry, radians, the unit circle, and complex numbers. | 10% |
Strategies for Mastering Difficult Math Concepts
Consistent practice with challenging problems ensures you are well-prepared for the most difficult questions in the digital SAT Math section.
Step-by-Step Process for Mastering Challenging Questions
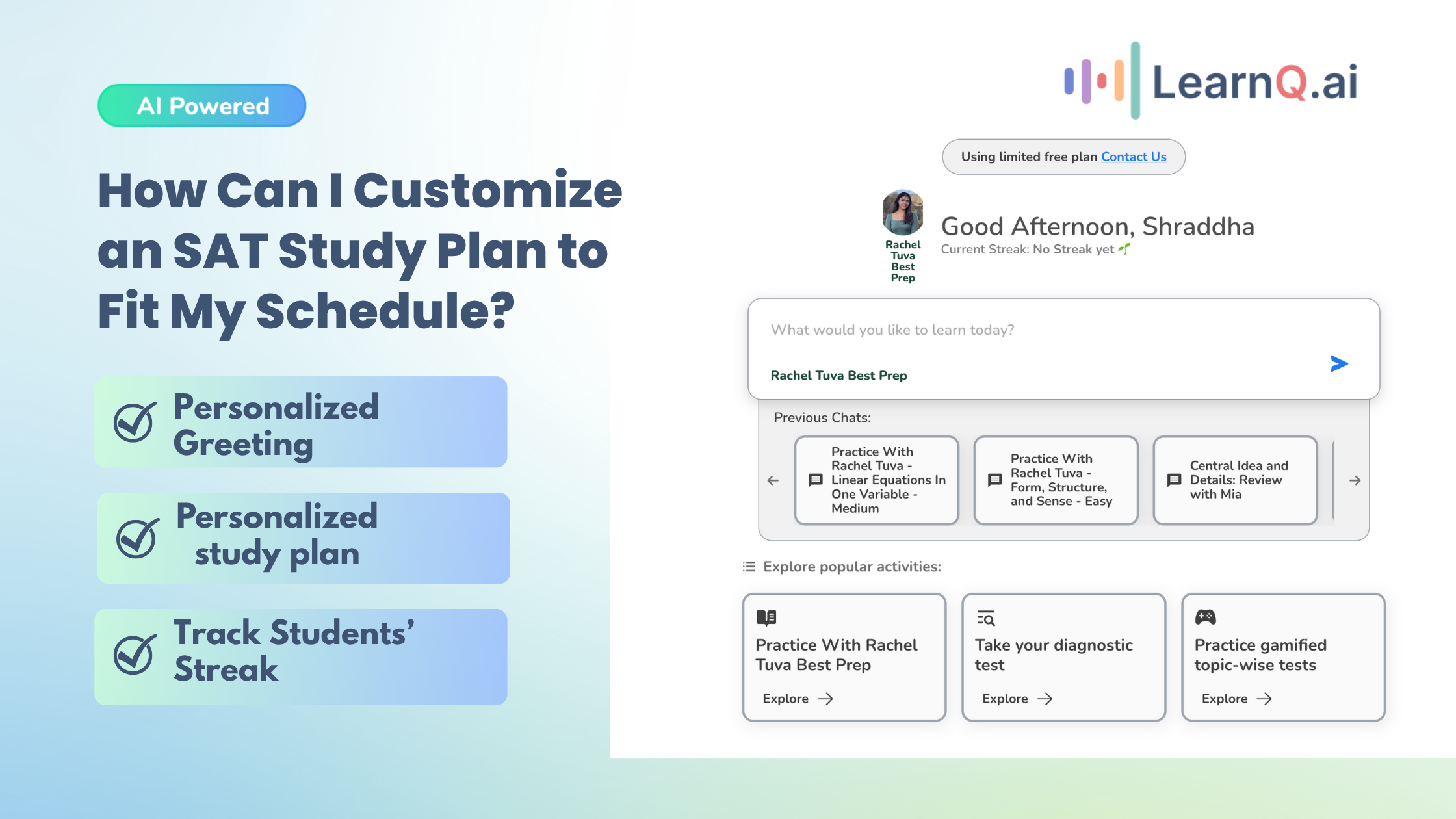
- Identify Weak Areas: Take a diagnostic test to pinpoint your weak areas. LearnQ.ai provides comprehensive diagnostic tests to help you identify your strengths and weaknesses.
- Understand the Fundamentals: Review and solidify your understanding of basic concepts before tackling advanced problems like algebra, geometry, and trigonometry fundamentals.
- Practice Regularly: Dedicate time for math practice. To work on the hardest SAT Math questions, use high-quality practice materials, such as those provided by LearnQ.ai.
- Analyze Mistakes: Review your answers thoroughly with the help of detailed explanations and find out the mistakes.
- Seek Help When Needed: If you’re stuck on a particular concept, don’t hesitate to ask for help from teachers, tutors, or online resources. At LearnQ.ai, you will get help from an AI tutor called MIA as well.
By following these strategies and utilizing resources from LearnQ.ai, you can master the most difficult math concepts and be well-prepared for the hardest SAT Math questions.
15 Complex Practice Questions to Prepare for High Scores in Digital SAT Math
Below are 15 challenging and hardest SAT Math questions and detailed explanations to help you understand the solutions.
1. Complex Number Multiplication
Question: What is the product of (3+4i) and (1−2𝑖)?
Solution:
Multiply each term in the first complex number by each term in the second complex number:
(3+4𝑖)(1−2𝑖)=3⋅1+3⋅(−2𝑖)+4𝑖⋅1+4𝑖⋅(−2𝑖)
Explanation:
Multiply the real parts: 3⋅1=3
Multiply the real part of the first number by the imaginary part of the second: 3⋅(−2𝑖)=−6𝑖
Multiply the imaginary part of the first number by the real part of the second: 4𝑖⋅1=4𝑖
Multiply the imaginary parts: 4𝑖⋅(−2𝑖)=−8i2
Since i2=−1
−8𝑖2=−8(−1)=8
Combine all parts:
3−6𝑖+4𝑖+8=3−2𝑖+8=11−2𝑖
Answer: 11−2i
2. Circle Geometry
Question: A circle has a radius of 10. A chord is 8 units from the center. How long is the chord?
Use the Pythagorean theorem to find the length of the chord.
Explanation:
Draw the radius to the midpoint of the chord, forming a right triangle with the radius, the perpendicular distance from the center to the chord, and half of the chord length.
Let the length of the chord be 𝑐.
The radius (hypotenuse) is 10, the perpendicular distance from the center to the chord is 8, and half of the chord is c/2.
Apply the Pythagorean theorem:
𝑟2=𝑑2+(c/2)2
102=82+(c/2)2
100=64+(c/2)2
Solve for 𝑐:
100-64=(c/2)2
36=(c/2)2
62=(c/2)2
6=(c/2)
c=1/2
Answer:
The length of the chord is 12 units.
3. Alegbraic Manipulation
Question: If 𝑥2+𝑦2=25 and 𝑥𝑦=12, what is (𝑥+𝑦)2
Solution: Use the identity (𝑥+𝑦)2=𝑥2+𝑦2+2𝑥𝑦
Explanation:
Given,
𝑥2+𝑦2=25 and 𝑥𝑦=12
Substitute these values into the identity: (𝑥+𝑦)2=𝑥2+𝑦2+2𝑥𝑦
(𝑥+𝑦)2=25+24=49
Answer: (𝑥+𝑦)2=49
4. Trignometric Identities
Question: If sin𝜃= 3/5 and 𝜃 is in the first quadrant, find cos𝜃.
Solution:
Use the Pythagorean identity sin2𝜃+cos2𝜃=1
Explanation:
Given,
sin𝜃= 3/5
sin2𝜃=(3/5)2=9/25
cos2𝜃=1−sin2𝜃=1−9/25=16/25
Since θ is in the first quadrant, cosθ is positive:
cos𝜃=4/5
Answer: cos𝜃=4/5
5. Polynomial Functions
Question: Given 𝑓(𝑥)=𝑥3−4𝑥, find the value of 𝑓′(𝑥) at 𝑥=2.
Solution:
Differentiate 𝑓(𝑥) to get 𝑓′(𝑥)
Explanation:
Differentiate 𝑓(𝑥)=𝑥3−4𝑥
𝑓′(𝑥)=3𝑥2−4
Evaluate 𝑓′(𝑥) at 𝑥=2
𝑓′(2)=3(2)2−4=12−4=8
Answer: 𝑓′(2)=8
LearnQ.ai is Powered by VEGA AI—Is your Institute Next?
Give students a Duolingo-style test-prep platform with Shopify-level customization for tutors and institutes.
6.Exponential Equation
Question: Solve for 𝑥 in 32𝑥−1=27
Solution:
Rewrite 27 as a power of 3 and solve the equation.
Explanation:
Express 27 as 33
32𝑥−1=33
Since the bases are the same, set the exponents equal:
2𝑥−1=3
Solve for 𝑥
2𝑥=3+1
2𝑥=4
x=2
Answer: 𝑥=2
7.Logarithmic Function
Question: If log2𝑥=5, what is x?
Solution: Rewrite the logarithmic equation in exponential form to solve for 𝑥.
Explanation:
Given log2𝑥=5, the logarithmic equation can be rewritten in its exponential form as:
𝑥=25
Calculate the value of 25
25=32
Answer:
𝑥=32
8.Probability
Question: What is the probability of rolling a sum of 7 on two six-sided dice?
Solution:
Identify all possible pairs of dice rolls that add up to 7 and calculate the probability.
Explanation:
The possible pairs are (1,6), (2,5), (3,4), (4,3), (5,2), (6,1).
There are 6 favorable outcomes.
The total number of possible outcomes when rolling two dice is 6×6=36
𝑃(sum of 7)=6/36=1/6
Answer: 1/6
9.Sequence
What is the 10th term of the arithmetic sequence 3, 7, 11, 15, …?
Use the formula for the nth term of an arithmetic sequence: 𝑎𝑛=𝑎1+(𝑛−1)𝑑
Explanation:
First term 𝑎1=3
Common difference 𝑑=4
The nth term formula is:
𝑎10=3+(10−1)×4
𝑎10=3+36=39
Answer:
𝑎10=39
10.Geometry
Question: Find the area of an equilateral triangle with a side length of 6.
Solution: Use the formula for the area of an equilateral triangle: A=34s2.
Explanation:
Given side length 𝑠=6
𝐴=3462
𝐴=3436=93
Answer: 93
11.Functions
Question: If 𝑓(𝑥)=2𝑥+3 and 𝑔(𝑥)=𝑥2 x2, find (𝑓∘𝑔)(2).
Solution: First, find 𝑔(2) and then apply 𝑓 to the result.
Explanation:
Calculate 𝑔(2):
𝑔(2)=22=4
Now, find 𝑓(𝑔(2))=𝑓(4)
𝑓(4)=2×4+3=8+3=11
Answer:
(𝑓∘𝑔)(2)=11
Enhance your Digital SAT study routine with AI-driven insights and personalized practice tests.
12.Systems of equation
Question: Solve the system:
2𝑥+3𝑦=7
4𝑥−𝑦=5
Solution: Use the substitution or elimination method to solve the system.
Explanation:
Multiply the second equation by 3 to align the coefficients of 𝑦:
(4𝑥−𝑦=5)X3
12𝑥−3𝑦=15
Add this to the first equation:
(2𝑥+3𝑦=7) + (12𝑥−3𝑦=15)
14𝑥=22
𝑥=2214
𝑥=117
Substitute x back into the first equation to find y:
2(x)+3y=7
(227)+3y=7
3y=7-227
3y=277
y=97
Answer:
x=117, y=97
13.Inequalities
Question: Solve for 𝑥: ∣2𝑥−3∣<5
Explanation:
The inequality ∣2𝑥−3∣<5 can be rewritten as:
−5<2𝑥−3<5
Add 3 to all parts:
−5+3<2𝑥<5+3
−2<2x<8
Divide by 2:
−1<𝑥<4
Answer: −1<𝑥<4
14.Geometry (Three-Dimensional)
Question: Find the volume of a sphere with a radius of 3.
Solution: Use the formula for the volume of a sphere: 𝑉=43𝜋𝑟3
Explanation:
Given radius 𝑟=3
𝑉=43𝜋(3)3
𝑉=43𝜋X27
𝑉=36𝜋
Answer: 𝑉=36𝜋
14.Geometry (Three-Dimensional)
Question: Find the volume of a sphere with a radius of 3.
Solution: Use the formula for the volume of a sphere: 𝑉=43𝜋𝑟3
Explanation:
Given radius 𝑟=3
𝑉=43𝜋(3)3
𝑉=43𝜋X27
𝑉=36𝜋
Answer: 𝑉=36𝜋
15.Advance Algebra
Question: If 𝑎+𝑏=3 and 𝑎𝑏=2, find the value of 𝑎3+𝑏3
Solution: Use the identity 𝑎3+𝑏3=(𝑎+𝑏)(𝑎2−𝑎𝑏+𝑏2)
Explanation:
Given,
𝑎+𝑏=3 and 𝑎𝑏=2,
and 𝑎2+𝑏2=(𝑎+𝑏)2−2𝑎𝑏
𝑎2+𝑏2=(3)2−2X2
𝑎2+𝑏2=9−4=5
Now, use the identity
𝑎3+𝑏3=(𝑎+𝑏)((a+b)2−3𝑎𝑏)
𝑎3+𝑏3=(3)((3)2−3X2)
𝑎3+𝑏3=(3)(9−6)
𝑎3+𝑏3=(3)(3)
𝑎3+𝑏3=9
Answer: 𝑎3+𝑏3=9

You can significantly improve your proficiency in tackling the hardest SAT Math questions by thoroughly understanding and practicing these detailed questions and solutions.
Unique Features of the Practice Platform
LearnQ.ai offers an innovative and comprehensive approach to preparing for the digital SAT Math section. With features designed to make learning fun, engaging, and highly personalized, students can effectively master complex math concepts. Here are the standout features of LearnQ.ai’s practice platform:
Feature | Description |
Gamification | Learn by playing games to make learning more enjoyable and interactive. |
Data-Driven Learning | Master concepts in a data-driven way to understand progress and improvement areas. |
24×7 Assistance | Resolve doubts anytime by asking Mia for round-the-clock support. |
Personalization | Understand concepts in a fun and engaging way with Mia. |
Smart Learning | Start with a free diagnostic test to craft a personalized study plan. |
SAT Exam Score Calculator | Digital SAT diagnostic test to track and predict SAT scores. |
AI Tutor | MIA, your AI tutor for DSAT, offers personalized tutoring and support. |
By utilizing these features, LearnQ.ai ensures you have all the tools to excel in the digital SAT Math section.
Also, read the Digital SAT Question Bank For Perfect Preparation and score well on the test.
LearnQ.ai is powered by VEGA AI—Is your institute next?
Offer students a Duolingo-style test-prep platform with Shopify-level customization for tutors and institutes.





Disclaimer
The SAT is a trademark of the College Board, which is not affiliated with and does not endorse these practice materials. The information provided in this guide is for educational purposes to assist students in preparing for the SAT exam.